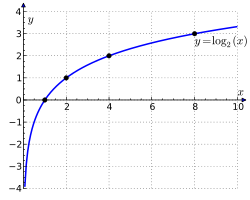
Graf funkcije dvojiški logaritem lb⁡x;0<x≤10displaystyle operatorname lb x,;,0<xleq 10

Dvojiški logaritem (ali binarni logaritem) je v matematiki logaritem z osnovo 2 (dvojiška osnova).^[1]:201 Je inverzna funkcija:

n↦2n.displaystyle nmapsto 2^n!,.

Dvojiški logaritem n je potenca na katero je treba dvigniti število 2, da se dobi vrednost n. Zaradi tega so dvojiški logaritmi primerni za računanja, ki vsebujejo potence od 2, na primer podvojitve.

ndisplaystyle n,	1	2	4	8	16	32	64	128	256
lb⁡ndisplaystyle operatorname lb n,	0	1	2	3	4	5	6	7	8

Dvojiški logaritem števila x je tako rešitev enačbe:

2a=x(n>0).displaystyle 2^a=xquad (n>0)!,.

Funkcija dvojiškega logaritma se označuje (glede na standard ISO 31-11) kot lb⁡xdisplaystyle operatorname lb x,, lb⁡(x)displaystyle operatorname lb (x), ali log2⁡xdisplaystyle log _2x,. Funkcija se označuje tudi kot ld⁡xdisplaystyle operatorname ld x, (po kratici latinskega imena logarithmus duālis, še posebej v nemških virih) ali lg⁡xdisplaystyle lg x,. lg⁡xdisplaystyle lg x, se še posebej pogosto rabi v teoriji števil. V TeX je običajno funkcija predefinirana z lg, za pravilni zapis »lb« ali zapis »ld« pa jo je treba na novo definirati s pomočjo operatorname.

Nadaljnji zgledi:

lb⁡0,5=−1;lb⁡3=1,584963;lb⁡π≈1,651496;lb⁡5π≈7,294552;lb⁡1256=−8displaystyle operatorname lb 0,5=-1;,operatorname lb 3=1,584963;,operatorname lb pi approx 1,651496;,operatorname lb 5^pi approx 7,294552;,operatorname lb frac 1256=-8

Uporaba |

Dvojiški logaritem npr. nastopa pri obrazcu za število enotskih lastnih vrednostih Redhefferjeve matrike. Velikokrat se rabi v računalništvu in teoriji informacij, saj je tesno povezan z dvojiškim številskim sistemom. Število števk (bitov) v dvojiški predstavitvi pozitivnega celega števila n je enako vsoti (spodnjega) celega dela n in 1, oziroma:

⌊lbn⌋+1.displaystyle lfloor operatorname lb ,nrfloor +1!,.

V teoriji informacij definicija količine lastne informacije in informacijske entropije vsebuje dvojiški logaritem. To je potrebno, ker se bit kot enota za informacijo nanaša na informacijo, ki izhaja iz pojavitve enega ali dveh enako verjetnih možnih dogodkov. Če se za računanje funkcij v teoriji informacij namesto dvojiškega logaritma rabi naravni logaritem loge⁡x≡ln⁡xdisplaystyle log _exequiv ln x,, se logaritemska naravna enota za informacijo, oziroma entropijo, imenuje nat. Če se rabi desetiški logaritem log10⁡x≡log⁡xdisplaystyle log _10xequiv log x,, je enota ban.

V programu za simbolno računanje Maple je dvojiški logaritem določen z log[2](n), v programu Mathematica pa z Log[2, z] in Log2[z].

Algebrske značilnosti |

Dvojiški logaritem narašča počasneje od katere koli potence števila xdisplaystyle x,.^[1]:201

Računanje |

Za računanje lb n na kalkulatorjih, ki nimajo te funkcije, se lahko uporabi naravni logaritem »ln« ali desetiški logaritem »log«. Obrazec za spremembo logaritemske osnove je:

lb⁡n=ln⁡nln⁡2=log⁡nlog⁡2,displaystyle operatorname lb n=frac ln nln 2=frac log nlog 2!,,

kjer je ln 2 naravni logaritem števila 2 z desetiško vrednostjo:

0,6931471805599453094172321214581765680755001343602552541206800094933...,^[2]

log 2 pa desetiški logaritem števila 2 z vrednostjo:

0,3010299956639811952137388947244930267681898814621085413104274611271...^[3]

Sklici |

Viri |

• 
  Stöcker, Horst (2006), Matematični priročnik z osnovami računalništva, Ljubljana: Tehniška založba Slovenije, COBISS 229576192, ISBN 86-365-0587-9 
  

Zunanje povezave |

• Weisstein, Eric Wolfgang. "Binary Logarithm" (angleščina). MathWorld.