수론과 조합론에서, 뫼비우스 함수(Möbius函數, 영어: Möbius function)는 정수가 제곱 인수가 없는 정수인지 여부에 따라 분류하는 곱셈적 함수이다. 뫼비우스 반전 공식에 사용되며, 리만 가설과도 깊은 관계를 가진다. 기호는 μ(n)displaystyle mu (n).

정의

뫼비우스 함수

μ:Z+→−1,0,+1displaystyle mu colon mathbb Z ^+to -1,0,+1

는 양의 정수 n∈Z+displaystyle nin mathbb Z ^+을 다음과 같이 −1,0,1displaystyle -1,0,1 가운데 하나에 대응시킨다.

• 
  ndisplaystyle n이 kdisplaystyle k개의 소인수를 갖는 제곱 인수가 없는 정수라면 μ(n)=(−1)kdisplaystyle mu (n)=(-1)^k이다. (특수한 경우로, n=1displaystyle n=1은 0개의 소인수를 가지므로 μ(1)=1displaystyle mu (1)=1이다.)


• 
  ndisplaystyle n이 제곱 인수가 없는 정수가 아니라면, μ(n)=0displaystyle mu (n)=0이다.

즉, ndisplaystyle n의 소인수 분해가

n=∏ppnpdisplaystyle n=prod _pp^n_p

라면, 뫼비우스 함수는 다음과 같다.

μ(n)=(−1)∑pnp∏p[np≤1]displaystyle mu (n)=(-1)^sum _pn_pprod _p[n_pleq 1]

여기서 [⋯]displaystyle [cdots ]는 아이버슨 괄호(조건이 참이면 1, 아니면 0)이다.

뫼비우스 함수 μ(n)displaystyle mu (n)은 또한 1의 원시적 ndisplaystyle n제곱근의 합이다.

μ(n)=∑1≤k≤ngcdk,n=1exp⁡(2πik/n)displaystyle mu (n)=sum _scriptstyle 1leq kleq n atop scriptstyle gcdk,n=1exp(2pi ik/n)

그렇기 때문에, 1보다 큰 임의의 자연수 n의 모든 약수에 대해서 μdisplaystyle mu 함숫값을 계산해서 더하면 언제나 0이 된다는 사실도 알 수 있다. 이 사실은 오일러 ϕdisplaystyle phi 함수에 대해, 임의의 자연수 n의 모든 약수의 ϕdisplaystyle phi 함숫값의 합은 언제나 n이 된다는 정리와 유사하다.

μdisplaystyle mu 는 양이 아닌 정수에 대하여 일반적으로 정의하지 않는다.

메르텐스 함수(Mertens函數, 영어: Mertens function)는 뫼비우스 함수의 부분합이다. 즉, 다음과 같은 함수이다.

M:Z+→Zdisplaystyle Mcolon mathbb Z ^+to mathbb Z

M(n)=∑k=1nμ(k)displaystyle M(n)=sum _k=1^nmu (k)

뫼비우스 함수는 1의 원시적 ndisplaystyle n제곱근의 합이므로, 메르텐스 함수를 다음과 같이 정의할 수도 있다.

M(n)=∑a∈Fnexp⁡(2πia)displaystyle M(n)=sum _ain mathcal F_nexp(2pi ia)

여기서 Fndisplaystyle mathcal F_n은 ndisplaystyle n차 페리 수열이다.

성질

뫼비우스 함수는 곱셈적 함수이다. 즉, 서로소 정수에 대하여 다음과 같다.

μ(ab)=μ(a)μ(b)(gcda,b=1)displaystyle mu (ab)=mu (a)mu (b)qquad (gcda,b=1)

뫼비우스 함수는 디리클레 합성곱 아래 상수 함수 1의 역원이다.

(μ∗1)(n)=∑d∣nμ(d)=δn,1={1n=10n>1displaystyle (mu *1)(n)=sum _dmid nmu (d)=delta _n,1=begincases1&n=1\0&n>1endcases

이 성질 때문에 뫼비우스 함수는 뫼비우스 반전 공식에 등장한다.

생성 함수

뫼비우스 함수의 생성 함수는 다음과 같다.

∑n=1∞μ(n)xn=x−∑a=2∞xa+∑a=2∞∑b=2∞xab−∑a=2∞∑b=2∞∑c=2∞xabc+∑a=2∞∑b=2∞∑c=2∞∑d=2∞xabcd−⋯displaystyle sum _n=1^infty mu (n)x^n=x-sum _a=2^infty x^a+sum _a=2^infty sum _b=2^infty x^ab-sum _a=2^infty sum _b=2^infty sum _c=2^infty x^abc+sum _a=2^infty sum _b=2^infty sum _c=2^infty sum _d=2^infty x^abcd-cdots

뫼비우스 함수의 람베르트 급수는 다음과 같다.

∑n=1∞μ(n)qn1−qn=qdisplaystyle sum _n=1^infty frac mu (n)q^n1-q^n=q

이는 |q|<1q에 대하여 수렴한다.

뫼비우스 함수의 디리클레 급수는 리만 제타 함수의 역수이다.

∑n=1∞μ(n)ns=1ζ(s)displaystyle sum _n=1^infty frac mu (n)n^s=frac 1zeta (s)

점근적 성질

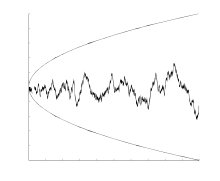
메르텐스 추측은 메르텐스 함수의 그래프가 포물선 속에 머무른다는 추측이다. 이는 작은 수에 대해서 성립하지만, 매우 큰 수에 대하여 성립하지 않는다.

뫼비우스 함수의 값이 ±1,0displaystyle pm 1,0뿐이므로, 메르텐스 함수는 매우 느리게 움직이며 또한 자명하게

|M(n)|≤n∀n∈Z+displaystyle

이다.

소수 정리에 따라 다음이 성립한다.

limn→∞1nM(n)=0displaystyle lim _nto infty frac 1nM(n)=0

또한, 다음이 성립한다.

limn→∞1n∑k=0n|μ(n)|=∏p(1−1p2)=1ζ(2)=6π2mu (n)

즉, 점근적으로 3/π2≈30.4%displaystyle 3/pi ^2approx 30.4%의 수에 대하여 뫼비우스 함수가 +1이며, 3/π2≈30.4%displaystyle 3/pi ^2approx 30.4%의 수에 대하여 뫼비우스 함수가 −1이며, 1−6/π2≈39.2%displaystyle 1-6/pi ^2approx 39.2%의 수에 대하여 뫼비우스 함수가 0이다.

리만 가설은 메르텐스 함수에 대한 다음 조건과 동치이다.

M(n)=O(x1/2+ϵ)∀ϵ∈R+displaystyle M(n)=O(x^1/2+epsilon )qquad forall epsilon in mathbb R ^+

메르텐스 추측(Mertens推測, 영어: Mertens conjecture)은 ∀n∈Z+:|M(n)|≤ndisplaystyle forall nin mathbb Z ^+colon 라는 명제이다. 이는 오랫동안 난제로 있었으나, 1985년에 거짓으로 판명되었으며, 다음이 성립한다.^{[1][2]:188–189}

lim infM(n)n<−1.009displaystyle liminf frac M(n)sqrt n<-1.009

lim supM(n)n>1.06displaystyle limsup frac M(n)sqrt n>1.06

그러나 리만 가설은 현재 (2016년) 미해결 문제이다. 메르텐스 추측보다 더 약하지만 리만 가설보다 더 강한 명제

M(n)=O(x1/2)displaystyle M(n)=O(x^1/2)

역시 아직 반증되지 않았으나, 이는 아마 거짓일 것이라고 추측된다.^[1]

급수

뫼비우스 함수에 대하여 다음과 같은 급수가 존재한다.

∑n=1∞(μ(n)/n)2=15/π2displaystyle sum _n=1^infty (mu (n)/n)^2=15/pi ^2

∑n=1∞μ(n)ln⁡nn=−1displaystyle sum _n=1^infty mu (n)frac ln nn=-1

표

처음 몇 개의 양의 정수에 대해서 뫼비우스 함수와 메르텐스 함수의 값은 다음과 같다. (OEIS의 수열 A008683), (OEIS의 수열 A002321)

ndisplaystyle n	1	2	3	4	5	6	7	8	9	10	11	12
μ(n)displaystyle mu (n)	1	−1	−1	0	−1	1	−1	0	0	1	−1	0
M(n)displaystyle M(n)	1	0	−1	−1	−2	−1	−2	−2	−2	−1	−2	−2

뫼비우스 함수의 값의 그래프는 다음과 같다.

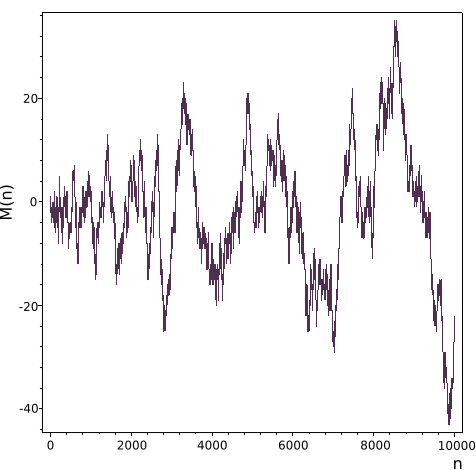
메르텐스 함수의 10⁴까지의 값의 그래프는 다음과 같다.

μ(n)=0displaystyle mu (n)=0인 정수 ndisplaystyle n (즉, 제곱 인수가 없는 정수가 아닌 수)은 다음과 같다.

4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, 32, 36, 40, 44, 45, 48, 49, 50, 52, 54, 56, 60, 63, … (OEIS의 수열 A013929)

역사

레온하르트 오일러는 1748년 저서^[3]에 뫼비우스 함수를 정의하고 암묵적으로 사용하였지만, 자세하게 다루지 않았다.^{[4]:99, Notes to §3.1} 1798년에 카를 프리드리히 가우스는 《산술 연구》(라틴어: Disquisitiones Arithmeticae)^[5]에서 1의 원시 ndisplaystyle n거듭제곱근의 합이 μ(n)displaystyle mu (n)이라는 것을 보였으나, 역시 이 함수를 특별히 연구하지 않았다.

1831년에 아우구스트 페르디난트 뫼비우스는 뫼비우스 함수를 최초로 명시적으로 도입하였다.^{[6][4]:99, Notes to §3.1} 1874년에 프란츠 메르텐스가 최초로 오늘날 사용되는 기호 μ를 사용하였다.^{[7]:53[4]:99, Notes to §3.1}

1885년 7월 11일에 토마스 요아너스 스틸티어스는 샤를 에르미트에게 보낸 편지에서 메르텐스 함수를 최초로 사용하였다. (이 편지는 1905년에 출판되었다.^[8]) 스틸티어스는 M(n)=O(n)displaystyle M(n)=O(sqrt n)임을 증명하였다고 주장하였고, 또 메르텐스 추측 (|M(n)|≤nleq sqrt n)을 추측하였다. 스틸티어스는 뫼비우스 함수를 f(n)displaystyle f(n)으로, 메르텐스 함수를 g(n)displaystyle g(n)으로 표기하였다. 이 편지에서 스틸티어스는 다음과 같이 적었다.

그러나 스틸티어스는 이 "증명"을 출판하지 않았다.

1897년에 프란츠 메르텐스는 메르텐스 함수를 독자적으로 재발견하였고, 메르텐스 추측을 스틸티어스와 독자적으로 추측하였다.^[9]

1985년에 앤드루 마이클 오들리스코(영어: Andrew Michael Odlyzko, 1949~)와 헤르마뉘스 요하너스 요서프 터 릴러(네덜란드어: Hermanus Johannes Joseph te Riele, 1947~)는 메르텐스 추측이 거짓임을 증명하였다.^[1]

같이 보기

• 뫼비우스 반전 공식


• 제곱 인수가 없는 정수


• 근접 대수


• 리만 제타 함수


• 프라임 제타 함수

참고 문헌

외부 링크

위키미디어 공용에 관련된 미디어 분류가 있습니다. 뫼비우스 함수

• 
  “Möbius function”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
  


• 
  Weisstein, Eric Wolfgang. “Möbius function”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
  


• 
  Weisstein, Eric Wolfgang. “Mertens function”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
  


• 
  Weisstein, Eric Wolfgang. “Mertens conjecture”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
  


• 
  Lipton, R. J. (2011년 2월 23일). “The depth of the Möbius function”. 《Gödel’s Lost Letter and P=NP》 (영어). 
  


• 
  Tao, Terence (2015년 9월 6일). “Sign patterns of the Möbius and Liouville functions”. 《What’s New》 (영어). 
  


• 
  “Möbius function”. 《OeisWiki》 (영어). 
  


• 
  “뫼비우스 뮤 함수”. 《오메가》. ^{[깨진 링크(과거 내용 찾기)]}